Melhorando Imagens com Filtro Homomórfico Usando OpenCV

Melhorando Imagens com Filtro Homomórfico Usando OpenCV

Quando trabalhamos com imagens, frequentemente nos deparamos com problemas de iluminação irregular que podem prejudicar a qualidade da imagem e dificultar a análise visual. Uma técnica eficaz para corrigir esses problemas é o uso de filtros homomórficos. Aqui, exploro como implementar um filtro homomórfico usando a biblioteca OpenCV em C++ para melhorar imagens com iluminação irregular.

O que é Filtragem Homomórfica?

A filtragem homomórfica é uma técnica usada para melhorar a aparência de imagens afetadas por variações de iluminação. Essa técnica atua no domínio da frequência e se baseia na transformação de Fourier para separar e manipular componentes de iluminação e refletância de uma imagem. A ideia é suavizar as variações de iluminação enquanto amplifica os detalhes da imagem.

Passos para Implementar o Filtro Homomórfico

1. Carregamento da Imagem

Primeiro, precisamos carregar a imagem em tons de cinza que será processada:

cv::Mat image = cv::imread(argv[1], cv::IMREAD_GRAYSCALE);
if (image.empty()) {
    std::cerr << "Error opening image: " << argv[1] << std::endl;
    return EXIT_FAILURE;
}

2. Padding da Imagem

A imagem é preenchida com zeros para garantir que seu tamanho seja adequado para a Transformada Rápida de Fourier (FFT):

int dft_M = cv::getOptimalDFTSize(image.rows);
int dft_N = cv::getOptimalDFTSize(image.cols);
cv::Mat paddedImage;
cv::copyMakeBorder(image, paddedImage, 0, dft_M - image.rows, 0, dft_N - image.cols, cv::BORDER_CONSTANT, cv::Scalar::all(0));

3. Transformada de Fourier (DFT)

Criamos uma imagem complexa com dois canais (Real e Imaginário) para aplicar a DFT:

std::vector<cv::Mat> planes;
cv::Mat zeros = cv::Mat_<float>::zeros(paddedImage.size());
cv::Mat realInput = cv::Mat_<float>(paddedImage);
realInput += cv::Scalar::all(1);
log(realInput, realInput);
planes.push_back(realInput);
planes.push_back(zeros);
cv::Mat complexImage;
cv::merge(planes, complexImage);
cv::dft(complexImage, complexImage);

4. Troca de Quadrantes

Para facilitar a visualização e o projeto do filtro, os quadrantes da imagem transformada são trocados:

void shiftDFT(cv::Mat &image) {
    cv::Mat tmp, topLeft, topRight, bottomLeft, bottomRight;
    int cx = image.cols / 2;
    int cy = image.rows / 2;
    topLeft = image(cv::Rect(0, 0, cx, cy));
    topRight = image(cv::Rect(cx, 0, cx, cy));
    bottomLeft = image(cv::Rect(0, cy, cx, cy));
    bottomRight = image(cv::Rect(cx, cy, cx, cy));
    topLeft.copyTo(tmp);
    bottomRight.copyTo(topLeft);
    tmp.copyTo(bottomRight);
    bottomLeft.copyTo(tmp);
    topRight.copyTo(bottomLeft);
    tmp.copyTo(topRight);
}
shiftDFT(complexImage);

5. Criação do Filtro Homomórfico

Criamos um filtro de frequência que ajusta a iluminação da imagem:

cv::Mat createHomomorphicFilter(double gammaL, double gammaH, double sharpC, double cutoff) {
    cv::Mat filter = cv::Mat(paddedImage.size(), CV_32FC2, cv::Scalar(0));
    cv::Mat tmp = cv::Mat(dft_M, dft_N, CV_32F);
    for (int i = 0; i < dft_M; i++) {
        for (int j = 0; j < dft_N; j++) {
            tmp.at<float>(i, j) = (gammaH - gammaL) * (1 - exp(-sharpC * ((pow(i - dft_M / 2, 2) + pow(j - dft_N / 2, 2)) / pow(cutoff, 2)))) + gammaL;
        }
    }
    cv::Mat components[] = {tmp, tmp};
    cv::merge(components, 2, filter);
    cv::normalize(filter, filter, 0, 1, cv::NORM_MINMAX);
    return filter;
}

6. Aplicação do Filtro

Multiplicamos a imagem transformada pelo filtro e aplicamos a Transformada Inversa de Fourier:

cv::Mat filter = createHomomorphicFilter(gammaL, gammaH, sharpC, cutoff);
cv::mulSpectrums(complexImage, filter, complexImage, 0);
shiftDFT(complexImage);
cv::idft(complexImage, complexImage);

7. Visualização da Imagem Filtrada

Finalmente, visualizamos a imagem filtrada:

std::vector<cv::Mat> planes;
cv::split(complexImage, planes);
exp(planes[0], planes[0]);
cv::normalize(planes[0], planes[0], 0, 1, cv::NORM_MINMAX);
cv::imshow("Homomorphic Filtered Image", planes[0]);

Resultados

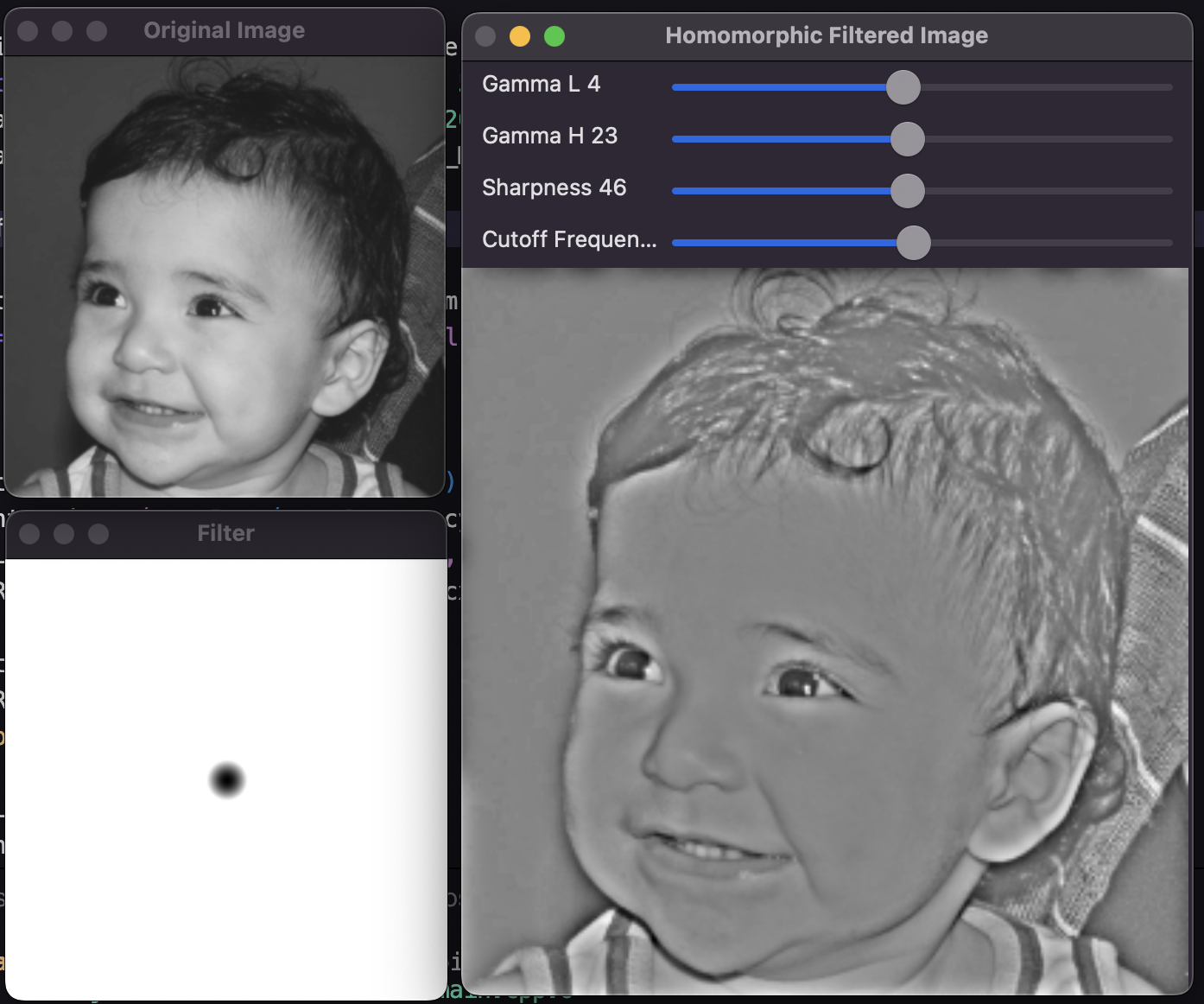
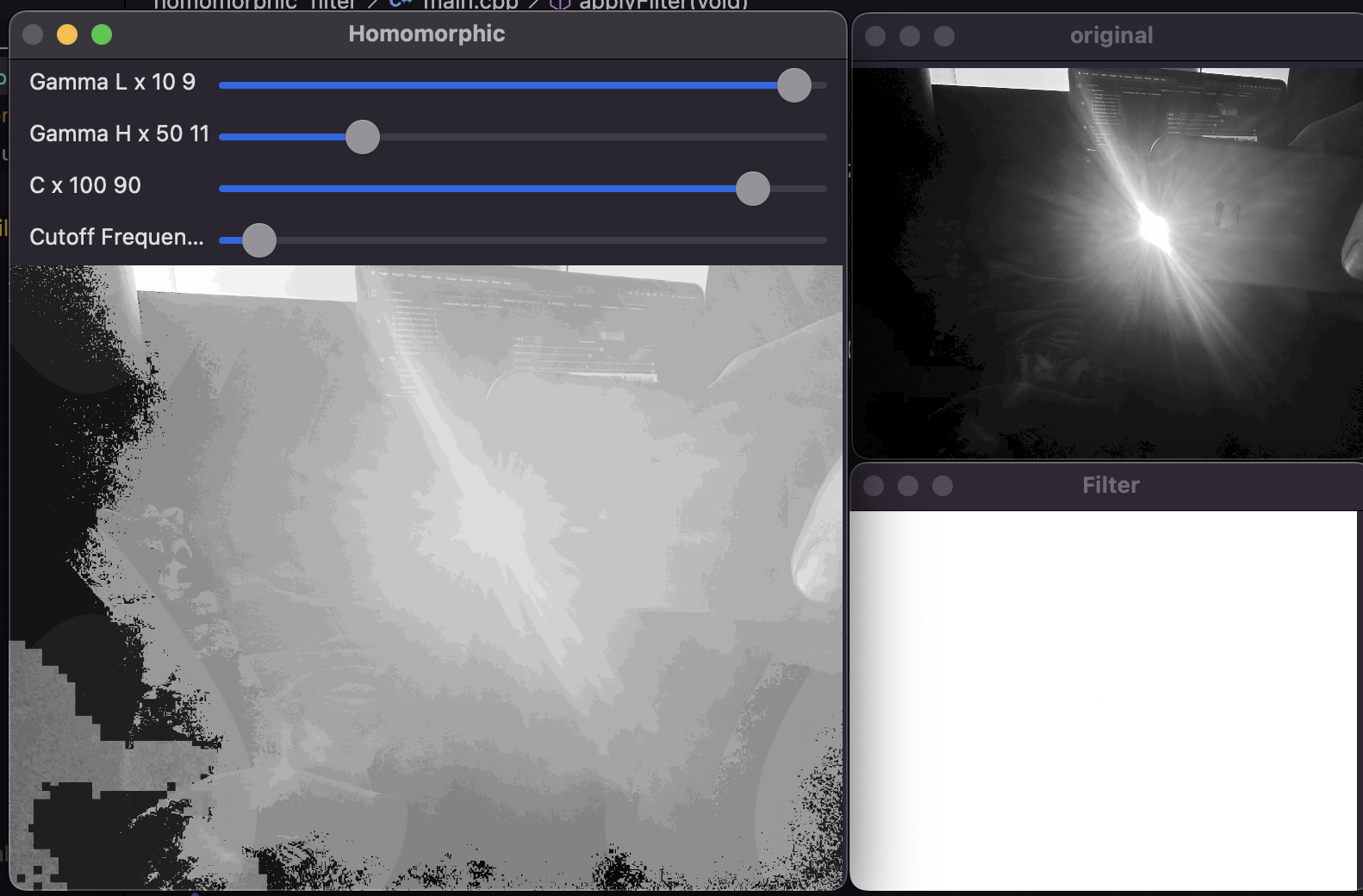
Veja abaixo alguns exemplos de imagens antes e depois da aplicação do filtro homomórfico:

Imagem Original	Imagem Filtrada

Conclusão

O filtro homomórfico é uma técnica poderosa para melhorar a qualidade de imagens com iluminação irregular. Ao aplicar esta técnica, conseguimos destacar detalhes importantes e corrigir variações de iluminação, resultando em imagens mais claras e uniformes. Com o código fornecido, você pode experimentar e ajustar os parâmetros para obter os melhores resultados para suas próprias imagens.